当我们在搜索引擎中输入关键字后,总会展开一个下拉列表,显示关键词相关的词汇以及内容。那么,这个搜索提示是如何实现的呢?今天总结的 Tire 树就可以实现这个功能。
Tire 树是什么
Tire 树也叫字典树。它是一个树形结构,专门用来处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题。
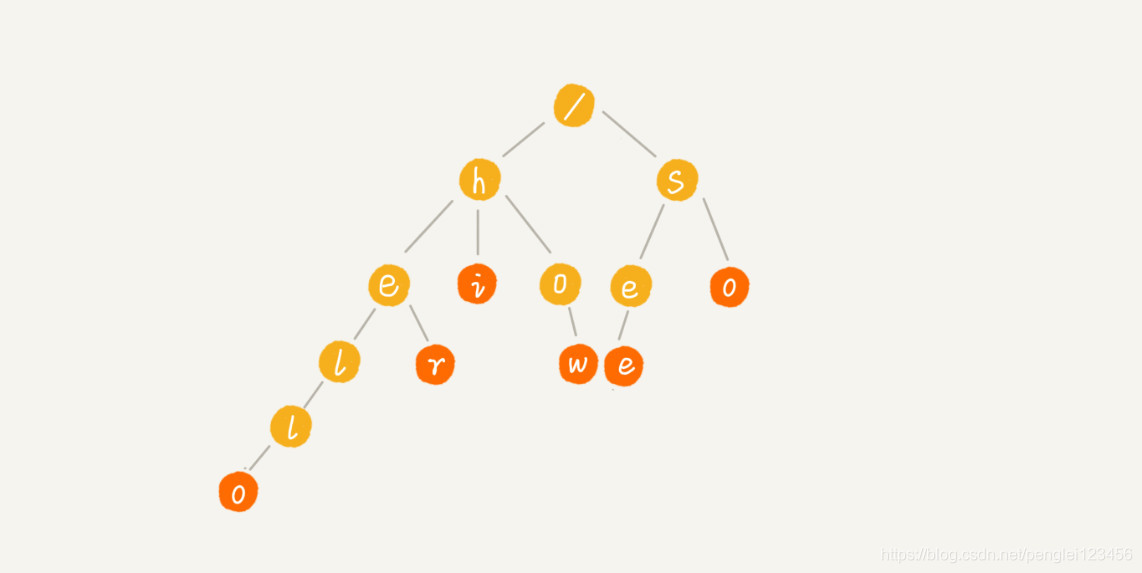
上图示用六个字符串构造一个 Tire 树。这六个字符串分别是:how,hi,her,hello,so,see。
该 Tire 树的详细构造过程请看下图: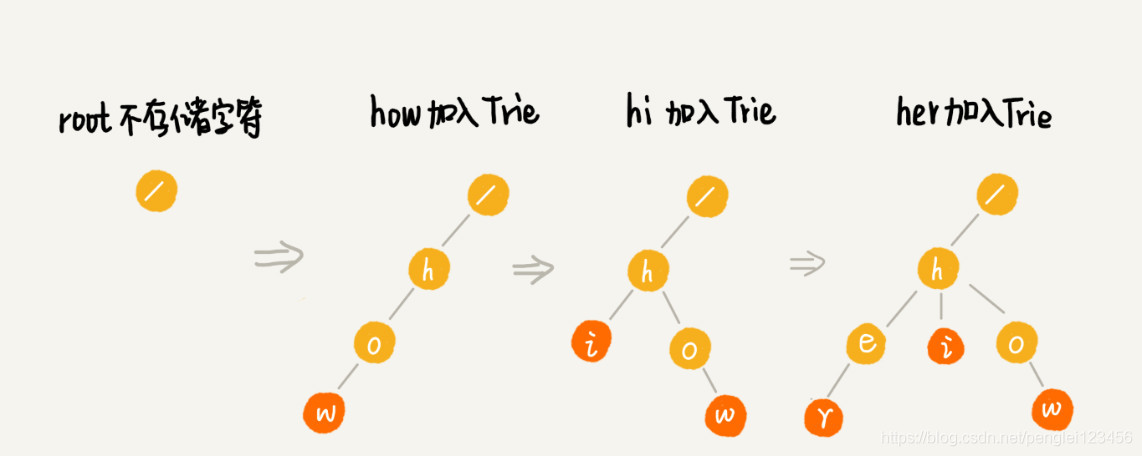
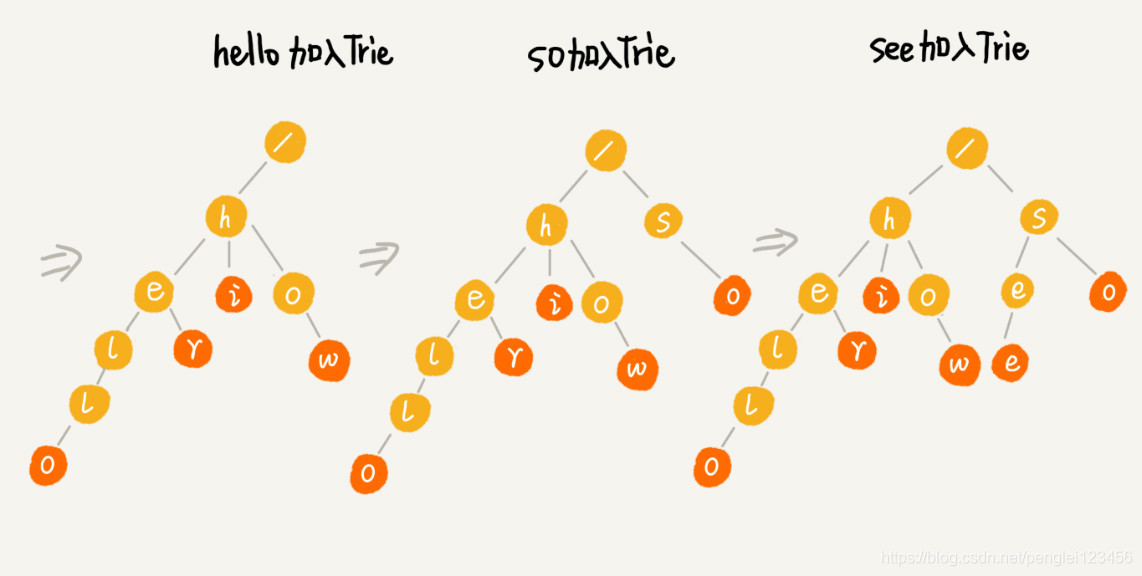
通过上面的举例说明,应该已经清楚的掌握了 Trie 树的结构以及构造过程。
如何实现一个 Tire 树
以前总结的二叉树,我们会构造一个节点,节点中有专门存储数据的变量,也有分别指向左子节点和右子节点的指针变量。但是对于一个 Tire 树(多叉树),如何构造指向子节点的指针变量呢?
采用一种经典的存储方式,类似于散列表。将字符集的所有字符与数组的下标一一映射,用数组的下标代替存储子节点的指针。例如 a - z 一共 26 个小写字母,我们就创建一个长度为 26 的数组。数组下标 0 的位置存储指向子节点 a 的指针,数组下标 1 的位置存储指向子节点 b 的指针b,数组下标 25 的位置存储指向子节点 z 的指针。那么,Tire 树中的节点表示就如下:1
2
3
4class TrieNode {
char data;
TrieNode children[26];
}
在 Tire 树中查找字符串的时候,我们可以利用字符的 ASCII 码减去字符 ‘a’ 的 ASCII 码,就能得到该字符所对应的数组中的下标。在 Tire 树中实现插入与查找的代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57public class Trie {
// 初始化根节点,存储无意义字符
private TrieNode root = new TrieNode('/');
// 往 Trie 树中插入一个字符串
public void insert(char[] text) {
//获取根节点
TrieNode p = root;
for (int i = 0; i < text.length; ++i) {
//求出text[i]字符对应数组中的下标
int index = text[i] - 'a';
//该下标下无子节点,插入子节点
if (p.children[index] == null) {
TrieNode newNode = new TrieNode(text[i]);
p.children[index] = newNode;
}
//重新复赋值 p 进行下一轮对比
p = p.children[index];
}
//设置字符串结束标志,说明从根节点到该层的节点,有一个完整的字符串
p.isEndingChar = true;
}
// 在 Trie 树中查找一个字符串
public boolean find(char[] pattern) {
//获取根节点
TrieNode p = root;
for (int i = 0; i < pattern.length; ++i) {
//求出pattern[i]字符对应数组中的下标
int index = pattern[i] - 'a';
//没有子节点,没有查找到该字符串,直接返回,
if (p.children[index] == null) {
return false; // 不存在 pattern
}
//重新复赋值 p 进行下一轮查找
p = p.children[index];
}
if (p.isEndingChar == false){
return false; // 不能完全匹配,只是前缀
}else{
return true; // 找到 pattern
}
}
public class TrieNode {
//数据存储
public char data;
//子节点存储
public TrieNode[] children = new TrieNode[26];
//结束标识
public boolean isEndingChar = false;
//初始化节点
public TrieNode(char data) {
this.data = data;
}
}
}
上述代码有详细的注释,足以明白整个过程。
如果在一组字符串中,频繁地查找某个字符串,则 Tire 树的效率是非常高的。构建一个 Tire 树,需要把字符串遍历一遍,所以时间复杂度是 O(n)。如果查找一个字符串,需要比较的次数就是该字符串的长度。所以,如果一个字符串长度为 k ,那么查找的时间复杂度就是 O(k)。
Tire 树的评估
Tire 树其实是很占用内存的。以上述存储 a - z 26个小写字母为例,每个子节点出了要存储自身的字符以外,还要额外开辟出 26 个字符存储的空间用来存储子节点。如果 Tire 树中的子节点都满了,那么对内存的利用率就高了。但是实际情况中可能只包含两三个子节点,所以内存浪费很严重。
优化的话,可以降低一下查询效率来节省存储空间。比如子节点的存储可以采用哈希表,红黑树,跳表等结构来实现。
Tire 树的四个限制
1:字符串的字符集不能太大,太大的话会造成严重的内存空间资源浪费。
2:要求字符串的前缀重合比较多,不然一样会造成内存空间资源浪费。
3:实现 Tire 树的过程比较复杂,这在工程上是把简单问题复杂化,不可取,除非必须。
4: Tire 树利用了指针存储,指针存储对内存是不友好的,降低了部分性能。
考虑到上面四个限制条件,我们在实际操作中,更偏向于运用散列表,跳表等结构实现字符串的查找。因为好多变成语言已经对此封装,可以便捷的拿来使用。
总结
本文创作灵感来源于 极客时间 王争老师的《数据结构与算法之美》课程,通过课后反思以及借鉴各位学友的发言总结,现整理出自己的知识架构,以便日后温故知新,查漏补缺。
初入算法学习,必是步履蹒跚,一路磕磕绊绊跌跌撞撞。看不懂别慌,也别忙着总结,先读五遍文章先,无他,唯手熟尔~
与诸君共勉