BM算法的核心思想
在上一篇的总结中,如果模式串和当前子串不匹配,则模式串和下一个子串进行比较,比较的时候会从第一个字母开始一个一个对比。
在上述的描述中,我们可以把模式串与子串的对比看作是模式串在主串上的滑动。如果当前对比不匹配,模式串就向后滑动一位,与新的子串进行对比。
这样的过程,每次模式串都是移动一位。但是再实际情况中,可能主串中的字符有 c,但是模式串中并不包含该字符。那么,模式串其实可以直接移动到不含字符 c 的那一段,这样模式串移动的距离增加了,提高了对比的效率。
请看如下图示: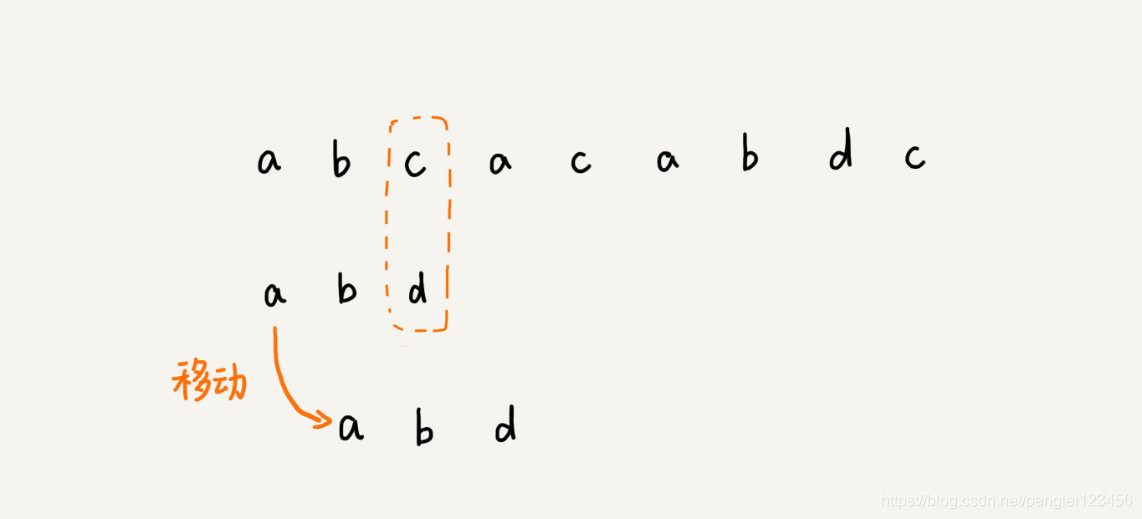
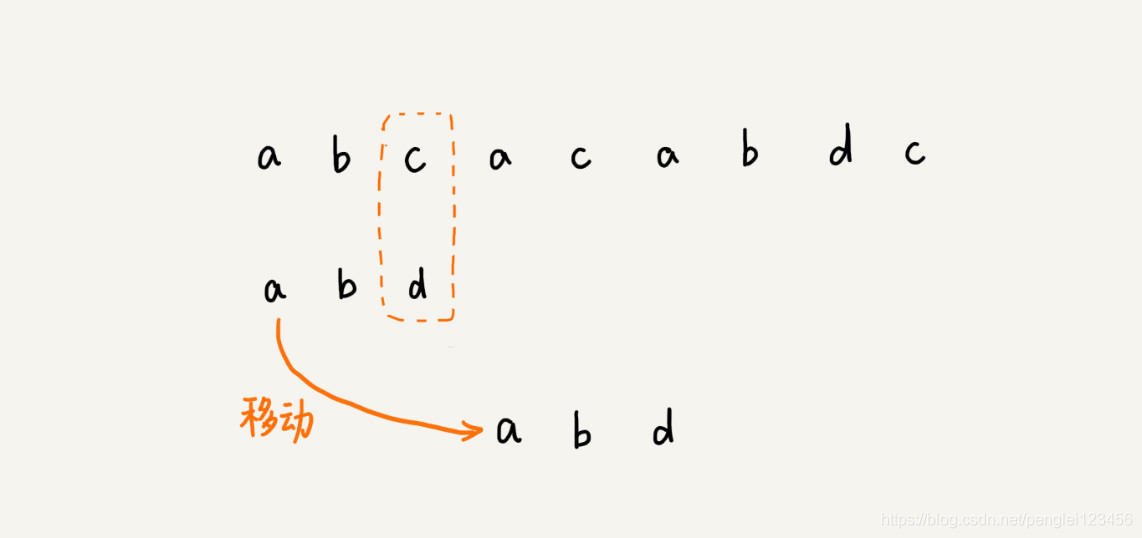
BM算法原理分析
BM 算法中包含两个重要的规则:坏字符规则和好后缀规则。
坏字符规则
一般的字符串匹配验证,是从第一个字符开始依次向后比较。而 BM 算法确事从最后一个字符向前一个一个比较。如下所示,我们会从模式串的最后一个字符开始比较:
a,b,c,a,c,a,b,d,c
a,b,d
模式串中的最后一个字符 d 与主串中的字符 c(坏字符) 不匹配,这个时候需要将模式串向后移动三位,彻底错开主串中的 c 字符:
a,b,c,a,c,a,b,d,c
————–a,b,d
继续对比,发现模式串中的字符 d 和主串中对应的字符 a(怀字符) 不匹配,这个时候需要将模式串向后移动两位,使得主串和模式串中的字符 a 相对应。
a,b,c,a,c,a,b,d,c
———————–a,b,d
通过上述过程得出以下规律:当发生不匹配的时候,我们把坏字符对应模式串中的下标位置记做 si。如果怀字符在模式串中存在,则在模式串中的下标位置记为 xi,如果不存在则 xi 值为 -1。那么模式串向后移动的位数就是 si - xi。
上述过程模式串第一次移动的时候,si = 2,xi = -1。
上述过程模式串第二次移动的时候,si = 2,xi = 0。
注意:如果怀字符在模式串中多次出现,那么 xi 的值取最靠近尾部的坏字符出现的位置。
仅仅根据坏字符规则是不能完全保证字符匹配的过程正确。例如主串为:aaaaaaaaaaaaaa,模式串为:baaaaa,那么模式串不仅不会向后移动,反而会向前移动。第一次移动的时候,si = 0,xi = 5。
好后缀规则
a,b,c,a,c,a,b,d,c,b,a,a,c,b,d,a,b
——————-b,d,b,d
观察上述对比,子串与模式串不匹配,模式串需要向后移动,移动的位数可以利用坏字符计算。但是,我们也可以换一种方法控制模式串的移动。
在上述对比过程中,我们发现子串中 bd(好后缀) 与模式串中的 bd 匹配上了,那么把 bd 记为{u}。此时我们拿着{u},在模式串中继续查找。当找到另一个{u}时,直接将模式串中的另一个{u}滑动到该位置,与{u}匹配,然后继续比较模式串和子串的字符。如果在模式串中没有找到{u},则直接将模式串滑动到最后。
a,b,c,a,c,a,b,d,a,b,d,a,c,b,d,a,b
——————-d,a,b,d
看上述对比,好后缀 bd 除了在模式串中的尾部匹配到以外,在其他位置并没有匹配到。但是这个时候却不能简单的将模式串滑动到好后缀的后面,这样的话就会错过了后面正好匹配上的子串。
当好后缀在模式串没有找到另外一处匹配的时候,只要模式串和好后缀重叠,那么模式串和子串就不可能完全匹配。但是,当模式串的头部和好后缀的尾部有重叠,并且重叠部分的字符正好匹配,那此时的主串和模式串就有可能完全匹配的上。可参考上面的字符匹配示意过程!
针对这种情况,我们要充分考虑好后缀的子串是否与模式串的头部字符串有相互匹配的上得情况。这个时候,我们就要考虑冲好后缀的子串中找到一个长度最长,并且能跟模式串的头部匹配上的子串。然后,将模式串向后移动,移动到模式串的头部和好后缀子串完全匹配上的地方。
针对好后缀的情况,我们同样可以采用坏字符的方式确定模式串滑动的位置。那么,如何恰当的运用这两种规则呢?如果同时满足这两种规则的话,通过计算比较一下两者需要模式串移动的距离,取其中移动距离最远的方式。
总结
代码实现不总结了,难度太大,至今还没研究透彻,留待日后补充吧。
本文创作灵感来源于 极客时间 王争老师的《数据结构与算法之美》课程,通过课后反思以及借鉴各位学友的发言总结,现整理出自己的知识架构,以便日后温故知新,查漏补缺。
初入算法学习,必是步履蹒跚,一路磕磕绊绊跌跌撞撞。看不懂别慌,也别忙着总结,先读五遍文章先,无他,唯手熟尔~
与诸君共勉