在实际开发过程中,总会遇到字符串匹配或者是包含的问题。而通用的编程语言中,基本上都有实现字符串匹配的方法。例如:Java 中的 indexof() 方法,底层的实现就是用的字符串匹配的算法。本文总结两种比较简单,容易理解的两种字符串比较算法:BF 算法和 RK 算法。
BF 算法
BF 算法,中文叫做暴力匹配算法,又叫朴素算法。
在 BF 算法中我们首先需要了解两个概念:主串和模式串。举个例子,如果我们要在字符串 A 中查找是否包含字符串 B,那么 A 就叫主串 B 就叫模式串。主串长度记为 n,模式串长度记为 m。
BF 算法中,我们分别在0,1,2… n-m 的位置检查长度为 m 的 n - m + 1 个子串,看看有没有跟模式串匹配的子串。检查过程图如下:
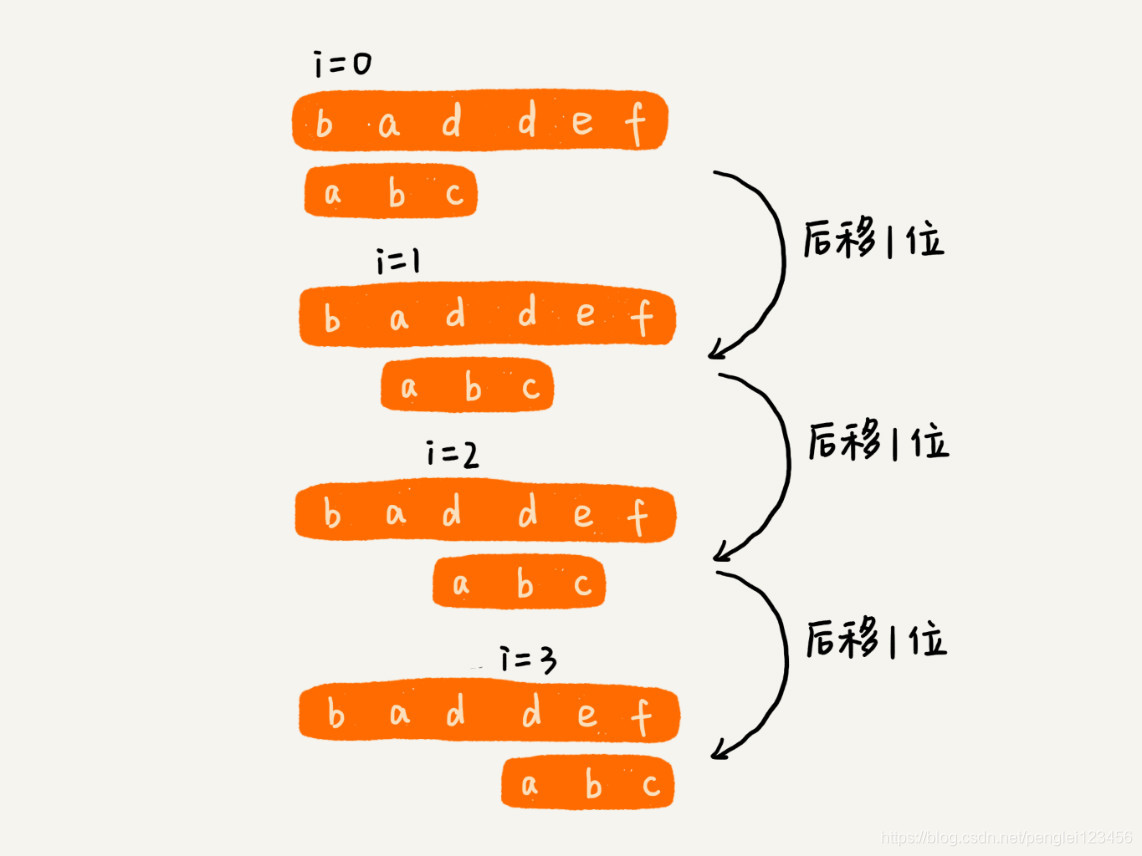
通过删除的过程,我们已经明白的 BF 算法执行的过程和原理。假如主串是 “aaaaaaaaaaaaaa”,模式串为 “aaaaab”,那么每次都要对别 m 的字符串,一共对比 n - m + 1 次。由此得出最坏情况下时间复杂度为 O(m * n)。
虽然 BF 算法的时间复杂度理论上很高,但是在实际情况中应用确是很多。主要是因为以下两种原因:1:实际业务中主串和模式串一般不会很长,都是很短的字符串,所以 O(n * m) 的时间复杂度是很小的。2:该算法实现起来简单,容易理解,所以出问题易排查。
RK 算法
在 BF 算法的基础上,我们引入哈希函数,就能降低它的时间复杂度,从而出现了 RK 算法。
RK 算法的思想:我们通过对主串中 n - m + 1 个子串哈希求值,然后对模式串也哈希求值,那么后续的比较就是关于哈希值的比较了(不考虑哈希冲突),降低了比较的时间复杂度。
比较的时间复杂度降低了,但是计算子串和模式串的哈希值依旧需要遍历每一个字符串,算法的整体时间复杂度没有提高。下面用一种巧妙的哈希算法提高计算哈希值的效率。
假设待比较的字符串的字符集包含 k 个字符,我们用一个 k 进制来表示一个子串,这个 k 进制转化为十进制,用来表示子串的哈希值。举例:如果我们的主串所在的字符集只有 a~z 的 26 个小写字母,那么我们用二十六进制表示字符串。a 对应 0,b 对应 1,一直到 z 对应 25。
下面上图解释如何用二十六进制表示子串: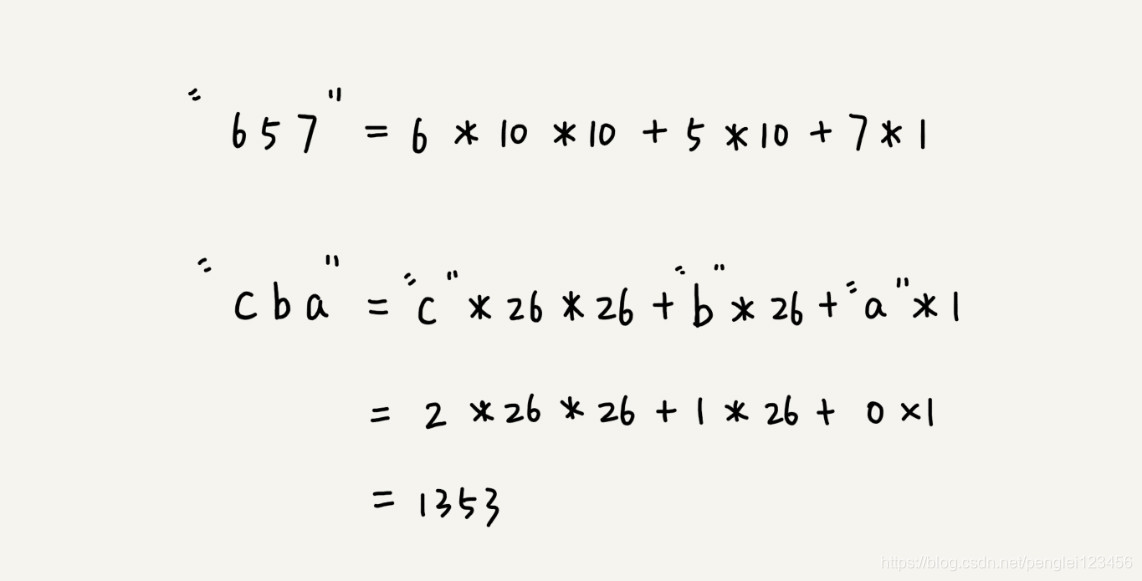
实际运用: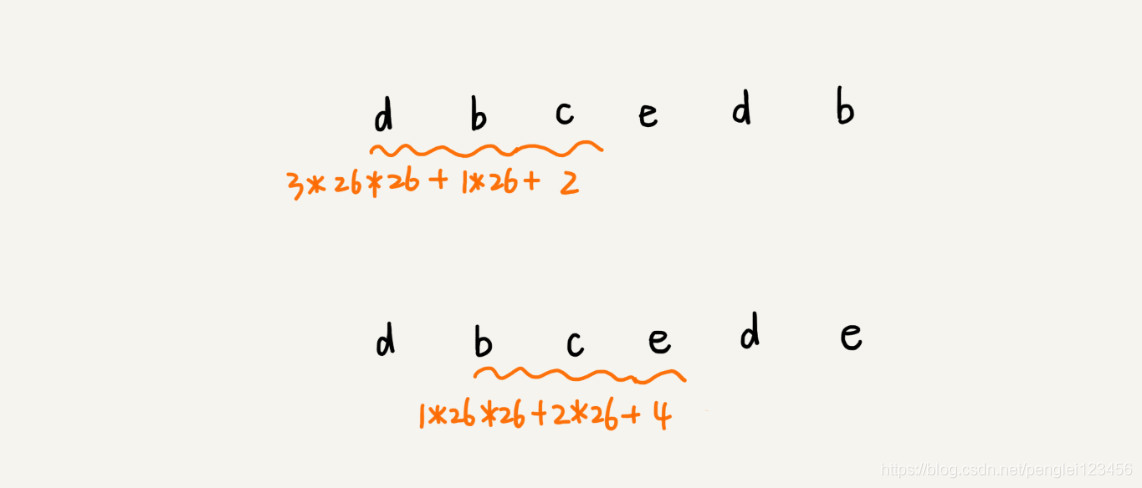
由上图得出规律:子串 s[i] 和子串 s[i - 1]是有关系的。i 代表子串开始的位置,子串的长度是 m。接下来我们推导出 子串 s[i] 和子串 s[i - 1] 之间哈希值的关系公式:1
2
3
4
5
6公式:
h[i] = 26*(h[i-1]-26^(m-1)*(s[i-1]-'a')) + (s[i+m-1]-'a');
解释:
h[i-1]-26^(m-1)*(s[i-1]-'a'):子串s[i-1]去掉第一个字符后的哈希值
(s[i+m-1]-'a'):子串s[i]最后一个字符的哈希值
其中, h[i]、h[i-1] 分别对应 s[i] 和 s[i-1] 两个子串的哈希值
在上述计算哈希值的过程中,26^0 ……26^(m - 1)的值,我们可以预先计算好存储起来,需要用的时候直接获取,不用每次计算。
RK 算法中,主要包含两部分:计算子串哈希值,子串与模式串哈希值的比较。第一部分,通过上述特殊设计的哈希算法,只需要扫描一次就能计算出所有子串的哈希值,时间复杂度为 O(n)。第二部分,子串与模式串的比较,总共比较 n - m + 1 次,所以时间复杂对 O(n)。所以,RK 算法的整体时间复杂度为 O(n)。
RK算法的补充
如果模式串很长,对应的子串就会也很长,哈希值有可能超出整形数据范围。
首先,上述哈希算法的设计是没有散列冲突的。因为我们是基于进制来表示字符串,所以是有限的字符串对应有限的哈希值,保证了不会散列冲突。
为了保证数据落入整形数据范围中,可以牺牲一下,适当的允许散列冲突。26 个小写字母依旧与 0 到 25 一一对应,当我们计算哈希值的时候,将所有字符串对应的数字相加,最后的结果作为哈希值。这样的设计,就保证最后的哈希值一定落在整形数据范围。
当哈希值冲突的时候,我们再对子串和模式串进行字符一一对比,这样就解决了哈希冲突。
所以,哈希函数的设计要保证冲突不能太高。如果极端情况下,子串的哈希值都冲突,那么就退化成子串与模式串的字符一一比较了,时间复杂度就退化成 O(n * m)。但是,一般情况下,只要冲突不多, RK 算法的时间复杂度还是小于 BF 算法的时间复杂度的。
总结
本文创作灵感来源于 极客时间 王争老师的《数据结构与算法之美》课程,通过课后反思以及借鉴各位学友的发言总结,现整理出自己的知识架构,以便日后温故知新,查漏补缺。
初入算法学习,必是步履蹒跚,一路磕磕绊绊跌跌撞撞。看不懂别慌,也别忙着总结,先读五遍文章先,无他,唯手熟尔~
与诸君共勉