算法笔记-堆排序

为什么说堆排序没有快速排序快

堆排序是一种原地的，时间复杂度为 O(nlogn) 的排序算法。

快速排序的时间复杂度也是 O(nlogn)，甚至堆排序比快速排序的时间复杂度还要稳定，但是快速排序的性能要比堆排序好。

什么是堆

堆是一个完全二叉树。

堆上任一节点的值都大于等于它的左右子树的值，或者小于等于它的左右子树的值。

对于每个节点大于等于子树的堆，叫做大顶堆。对于每个节点小于等于子树的堆，叫做小顶堆。

图例如下：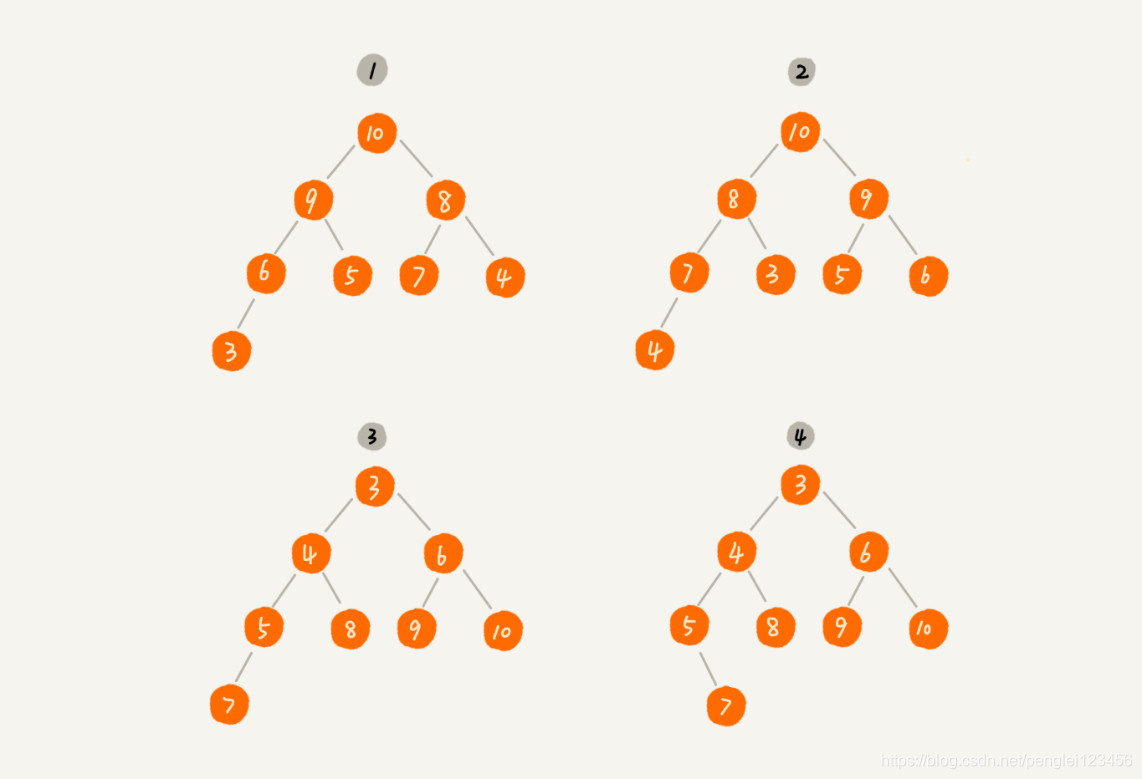

1，2，3属于堆排序，4不属于堆排序。

实现堆

在总结树那一篇文章中，提到完全二叉树适合用数组的方式存储数据。所以，对于堆这种完全二叉树，也用数组来存储。

图例如下：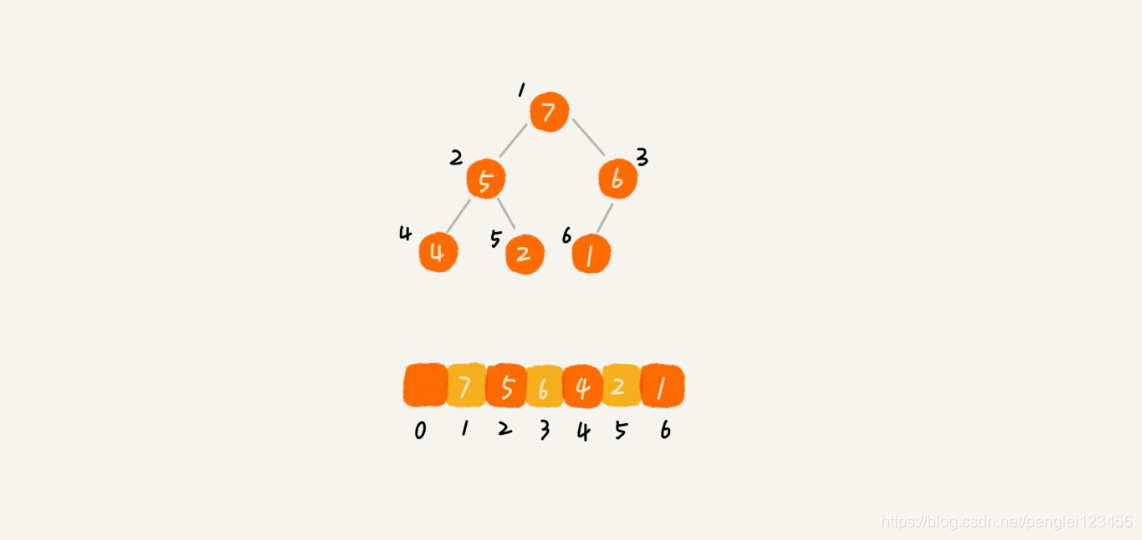

回顾一下存储规则：数组下标为 i 的节点，它的左子节点的下标为 2i，它的右左子节点的下标为 2i+1，它的父节点的下标是 i/2。

• 堆中插入元素：

  往堆中插入元素的时候，需要调整元素的位置保证满足堆的两个特性，这个过程就叫做堆化。堆化就是顺着节点的路径向上或者向下对比，交换。

下面是一张堆化的过程图：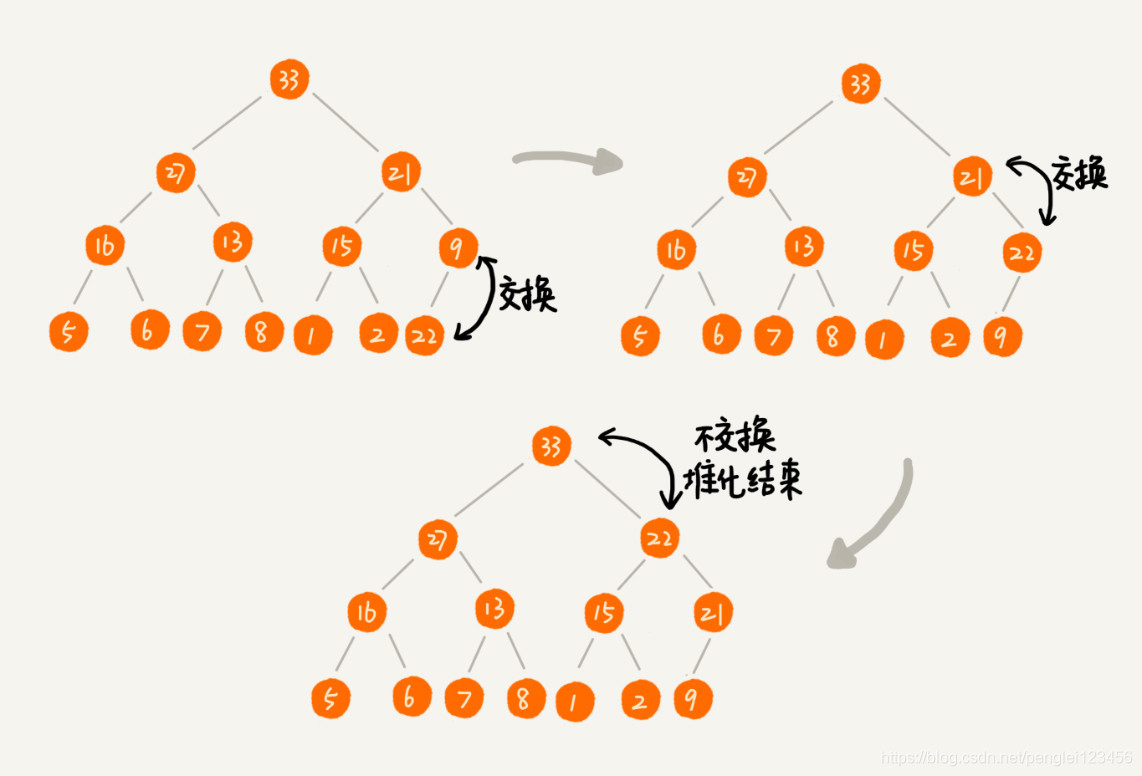

代码实现如下：

public class Heap {
	  private int[] heapList; 	// 数组，从下标 1 开始存储数据
	  private int n;  			// 堆中可存储的数据个数
	  private int count; 		// 堆中已经存储的数据个数

	  public Heap(int length) {
		heapList = new int[length + 1];
	    n = length;
	    count = 0;
	  }

	  public void insert(int data) {
	    if (count >= n) {
	    	return; // 堆满了
	    }
	    count++;
	    heapList[count] = data;
	    int i = count;
	    while (i/2 > 0 && heapList[i] > heapList[i/2]) { // 自下往上堆化
	      swap(heapList, i, i/2);
	      i = i/2;
	    }
	  }
	  
	  //交换
	  public void swap(int[] list, int i, int j){
		  int temp = list[i];
		  list[i] = list[j];
		  list[j] = temp;
	  }  
	  
 }

• 堆中删除堆顶元素：

  删除堆顶元素的时候，我们把最后一个元素放在堆顶，然后自上往下堆化。由于堆化的过程就是比较，交换，所以堆化之后，该树还会保持完全二叉树的结构。

  图例如下：
  

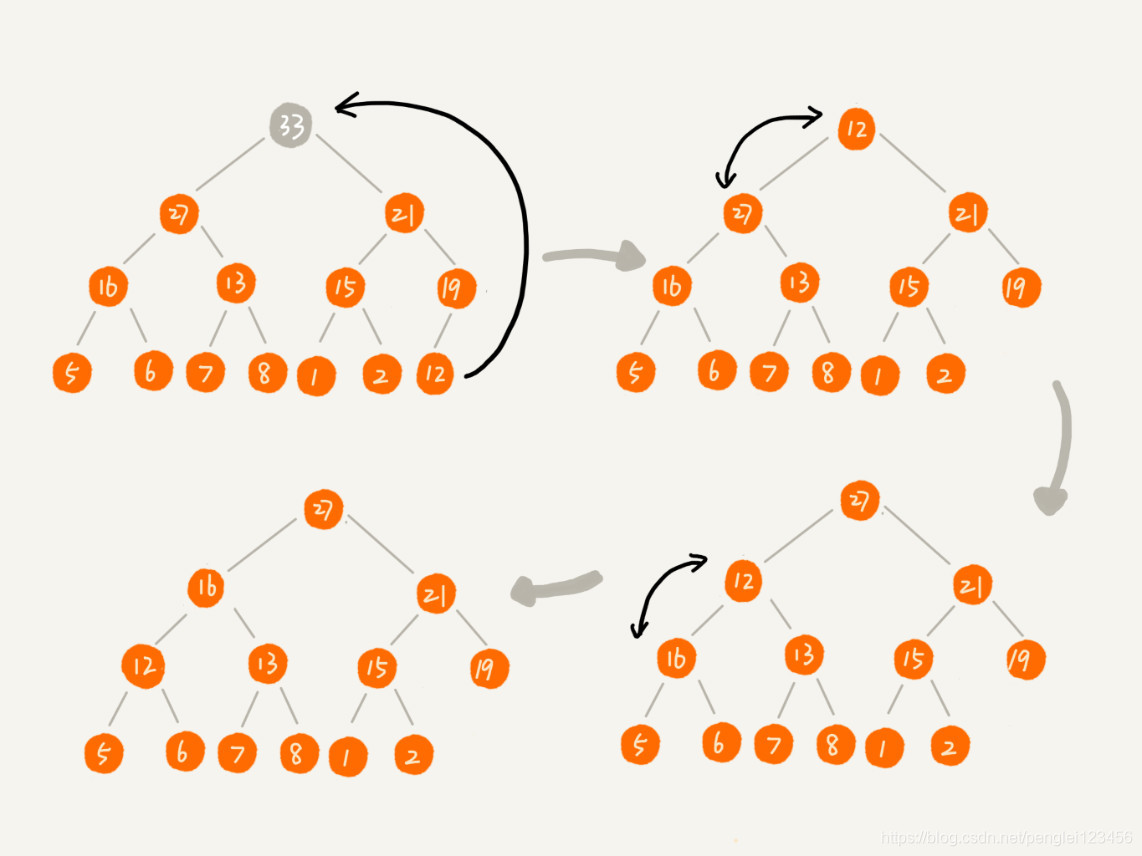
  代码如下：

  public class Heap {
  	  private int[] heapList; 	// 数组，从下标 1 开始存储数据
  	  private int n;  			// 堆中可存储的数据个数
  	  private int count; 		// 堆中已经存储的数据个数
  
  	  public Heap(int length) {
  		heapList = new int[length + 1];
  	    n = length;
  	    count = 0;
  	  }
  
  	  public void removeMax() {
  		  if (count == 0){
  			  return ;
  		  }
  		  heapList[1] = heapList[count];
  		  count--;
  		  heapify(heapList, count, 1);
  		}
  
  	  public void heapify(int[] heapList, int n, int i) { // 自上往下堆化
  		  while (true) {
  		    int maxPos = i;//当前要进行对比交换的元素下标
  		    //有左子节点，且小于左子节点
  		    if (i*2 <= n && heapList[i] < heapList[i*2]){
  		    	maxPos = i*2;
  		    } 
     		    /**
  		     * 这里 heapList[i] 替换成了 heapList[maxPos]
  		     * 如果第一个条件判断执行了，那么本次对比就是对比 左右节点的大小
  		     * 如果第一个条件判断没有执行，那么本次对比就是对比 父节点和右子节点
  		     */
  		    if (i*2+1 <= n && heapList[maxPos] < heapList[i*2+1]){
  		    	maxPos = i*2+1;
  		    } 
  		    //均大于左右子节点
  		    if (maxPos == i){
  		    	break;
  		    } 
  		    swap(heapList, i, maxPos);
  		    i = maxPos;
  		  }
  	  }
  	  
  	  //交换
  	  public void swap(int[] list, int i, int j){
  		  int temp = list[i];
  		  list[i] = list[j];
  		  list[j] = temp;
  	  }  
  	  
   }

基于堆实现排序

堆排序的时间复杂是 O(nlogn)，而且还是原地排序。

• 首先：建堆。

  第一种方法：我们利用的是往堆中插入元素的方法。起初，假设堆中只有一个元素，然后从数组下标 2 开始，依次往堆中插入元素，直至第 n 个元素。这样，我们就完成了建堆。这是从前往后处理数组，自下而上的堆化。

  第二种方法：利用的是删除堆顶元素后堆化的方法。因为自上而下的堆化，叶子节点没有左右节点，无法向下对比，所以我们从最后一个非叶子节点开始堆化。然后，一次堆化后续的叶子节点，最终实现了堆化。

  第二种方法的图例：
  
  

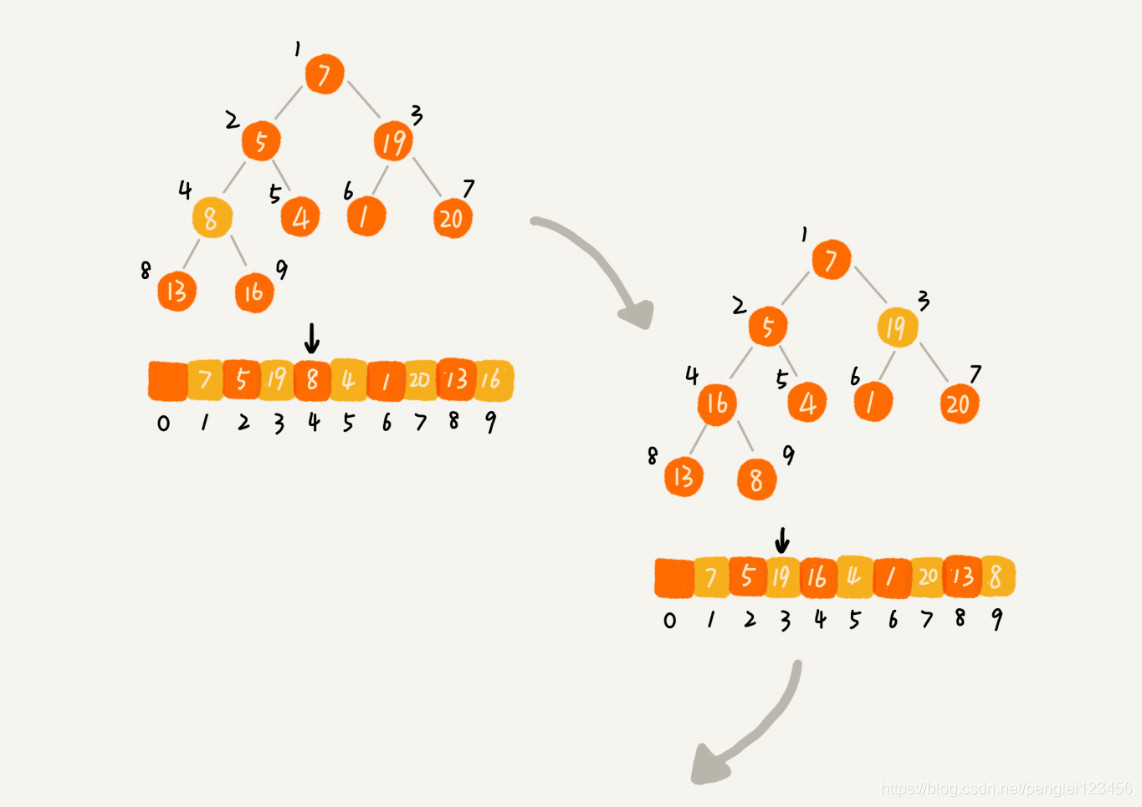
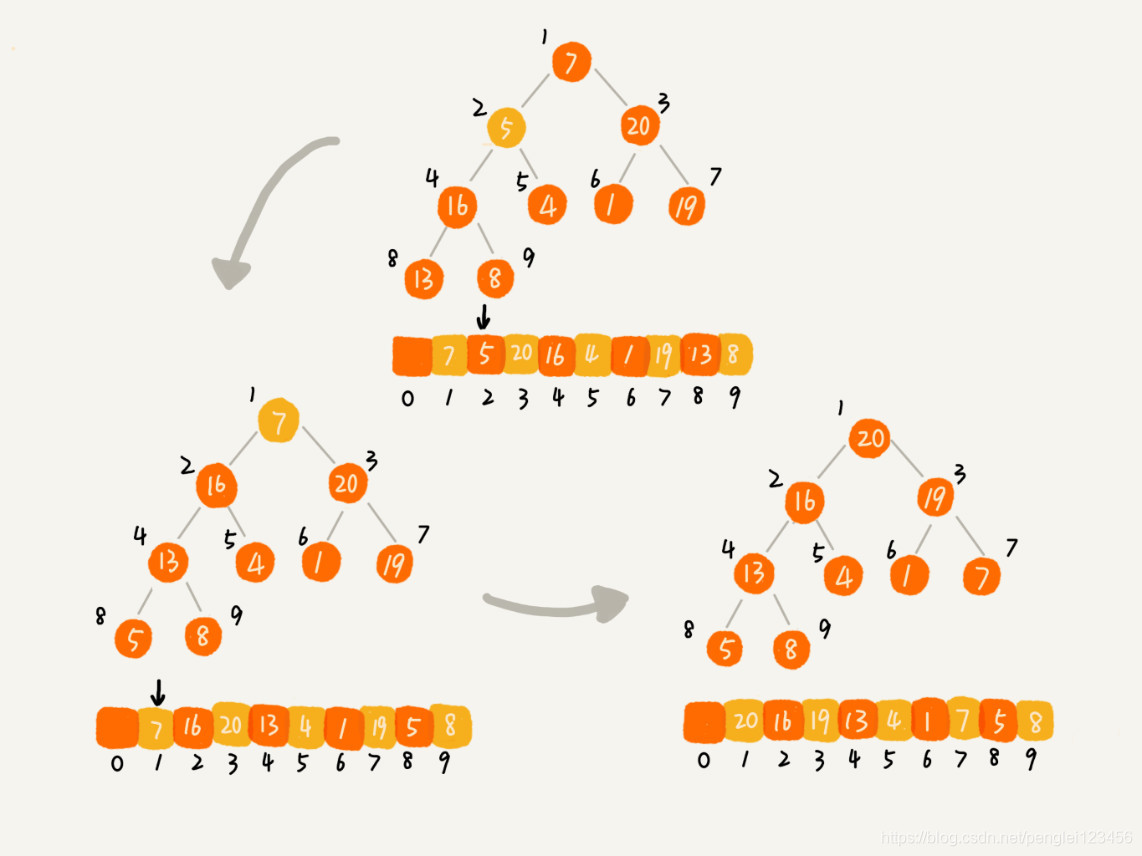
  直接得结论：建堆的时间复杂度是 O(n)。

• 其次：排序

  建堆完成之后，我们的堆是大顶堆，堆顶存储的就是最大的元素。

  排序过程还是用到了删除堆顶元素的方法。删除的时候，我们将数组的最后一个元素放在堆顶，然后继续堆化。但是排序的时候，我们将堆的最后一个元素和堆顶元素交换，然后对数组中剩下的 n - 1 个元素进行堆化。堆化结束后，我们继续把堆顶元素与堆的最后一个元素交换，然后继续对剩下的 n - 2 个元素堆化。如此往复，直至堆中只剩下最后一个元素，排序完成。

  直接得结论，堆排序的时间复杂度是：O(nlogn)

堆排序与快速排序的对比

1：堆排序是跳着访问数组中的元素，而快速排序是顺序访问，所以堆排序堆内存不友好。

2：在排序的过程中，堆排序的交换过程要远远大于快速排序的交换过程。

总结

后面的总结也是越来越难了。王老师开课之初，每节课下面的留言好多好多，每次学完文章都会翻阅留言。当时留言的质量也很高，留言区完全就是一个补充解惑的一个地方。到了现在的课程，留言数已经很少了，好多同学应该是学到这里就掉队了。

我也渐渐感到很大的压力了，虽然依旧能读懂，但是明显很吃力了。继续加油吧，如此由浅入深，循序渐进的优质课程少之又少，继续坚持下去。

本文创作灵感来源于 极客时间 王争老师的《数据结构与算法之美》课程，通过课后反思以及借鉴各位学友的发言总结，现整理出自己的知识架构，以便日后温故知新，查漏补缺。

初入算法学习，必是步履蹒跚，一路磕磕绊绊跌跌撞撞。看不懂别慌，也别忙着总结，先读五遍文章先，无他，唯手熟尔~
与诸君共勉