算法笔记-二叉树1

什么样的二叉树适合用数组来存储

前面的一系列文章主要总结的是线性数据结构，从今天开始，总结非线性数据结构的知识点。比如：树。

树

先看图：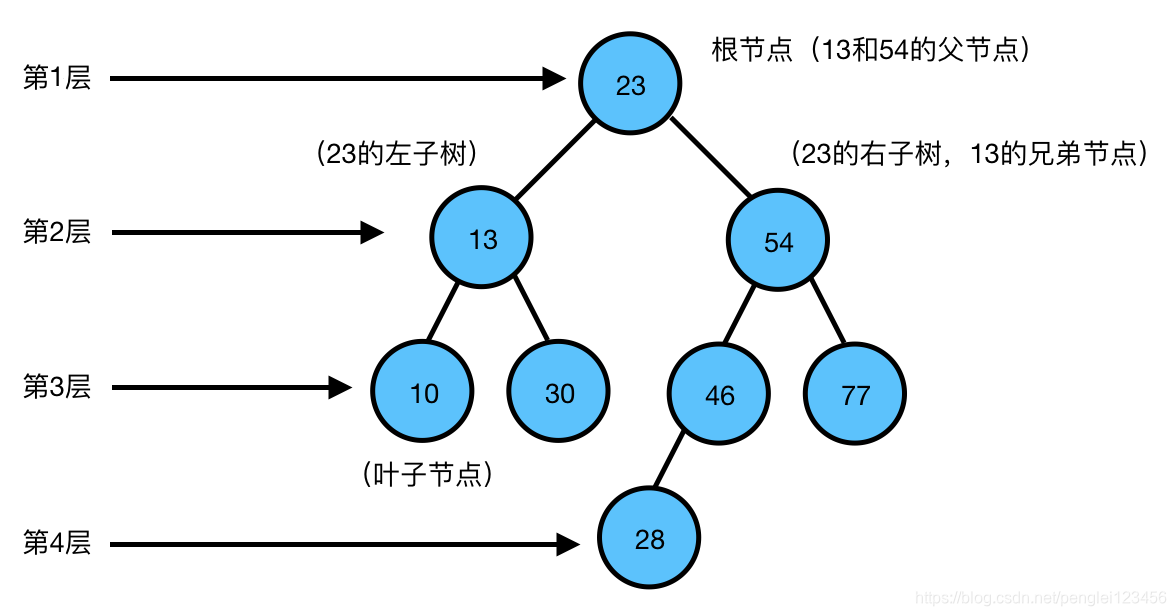

通过上面的图，可以很直观的理解以下概念：根节点，子节点，兄弟节点，叶子节点。

没有父节点的节点叫做根节点，比如节点 23。拥有相同的父节点的节点，称之为兄弟节点，比如节点 13 和节点 54。没有子节点的节点叫做叶子节点，比如节点 10，节点 28 等。

层级：如图所示，从 1 层开始，自上而下依次排序。
深度：从 0 开始，自上而下依次排序。节点的层级减一就是该节点的深度。
高度：从 0 开始，自下而上依次排序。高度与深度排序正好相反。

二叉树

树中的每个节点最多只能有两个子节点，分别是左子节点和右子节点。

满二叉树：叶子节点全在最底层，除了叶子节点以外，其他节点分别都有左子节点和右子节点。
满二叉树图例如下：

完全二叉树：叶子节点在最底下两层，最后一层的叶子节点靠左排列，除了最后一次，其他层的节点个数要达到最大数。
完全二叉树图例如下：

表示二叉树

链式存储法：每个节点包含三个内存域，一个用来存储数据，一个是左指针，指向左子节点的内存地址，一个是右指针，指向右子节点的内存地址。
如下图例：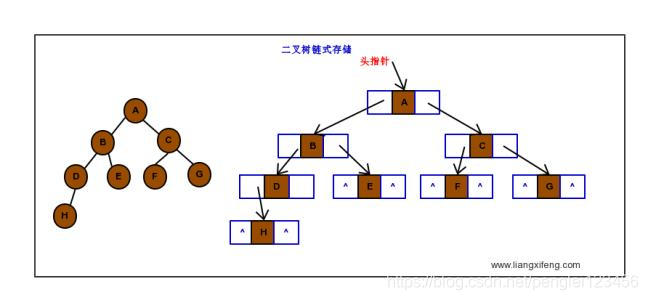

顺序存储法：基于数组实现的存储法。根节点存储在数组下标 i = 1 的位置，它的左子节点对应的数组下标就是 i 2 = 2， 右子节点对应的数组下标就是 i 2 + 1 = 3。依次类推，任意一个节点的左子节点对应的数组下标都是 i 2，右子节点对应的数组下标都是 i 2 + 1。
如下图例：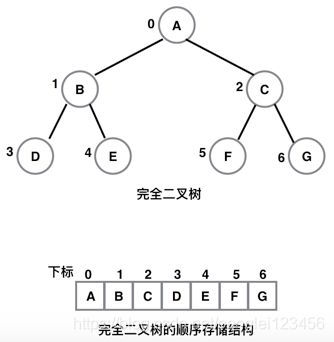

二叉树的遍历

插图：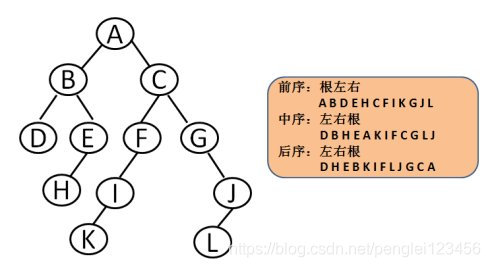

前序遍历：对于任意一个节点，先打印自身，然后打印左子节点，最后打印右子节点。
代码示例如下：

//前序遍历
public static void preOrder(TreeNode tree){
    System.out.println(tree.data);
    TreeNode leftNode = tree.leftNode;
    if(leftNode != null){
        preOrder(leftNode);
    }
    TreeNode rightNode = tree.rightNode;
    if(rightNode != null){
        preOrder(rightNode);
    }
}

中序遍历：对于任意一个节点，先打印左子节点，然后打印自身，最后打印右子节点。
代码示例如下：

//中序遍历
public static void middleOrder(TreeNode tree){
    TreeNode leftNode = tree.leftNode;
    if(leftNode != null){
        preOrder(leftNode);
    }
    System.out.println(tree.data);
    TreeNode rightNode = tree.rightNode;
    if(rightNode != null){
        preOrder(rightNode);
    }
}

后序遍历：对于任意一个节点，先打印左子节点，然后打印右子节点，最后打印自身。
代码示例如下：

//中序遍历
public static void postOrder(TreeNode tree){
    TreeNode leftNode = tree.leftNode;
    if(leftNode != null){
        preOrder(leftNode);
    }
    TreeNode rightNode = tree.rightNode;
    if(rightNode != null){
        preOrder(rightNode);
    }
    System.out.println(tree.data);
}

总结

本文创作灵感来源于 极客时间 王争老师的《数据结构与算法之美》课程，通过课后反思以及借鉴各位学友的发言总结，现整理出自己的知识架构，以便日后温故知新，查漏补缺。

初入算法学习，必是步履蹒跚，一路磕磕绊绊跌跌撞撞。看不懂别慌，也别忙着总结，先读五遍文章先，无他，唯手熟尔~
与诸君共勉