归并排序，快速排序

本文创作灵感来源于极客时间王争老师的《数据结构与算法之美》课程，通过课后反思以及借鉴各位学友的发言总结，现整理出自己的知识架构，以便日后温故知新，查漏补缺。

归并排序

归并排序的算法思路：将待排序的数组一分为二，然后分别对两段数组排序，然后合并两段有序数组。
归并排序的核心思想就是分治思想，分而治之。先将大问题一步一步分解成小问题，然后对小问题求解，所有的小问题解决掉之后，大问题也就解决掉了。其中分治的概念就让我们联想到递归，分治是思想，递归是代码实现，分对应了递，治对应了归。
归并排序就是在实现递归的逻辑。实现递归的逻辑，我们首先要推导出递归公式，以及终止条件。公式：sort(list[p,q]) = merge(sort(list[p,r]),sort(list[r+1,q]))，终止条件：p >= r。对公式进行下解释，sort 归并排序函数，merge 合并两个有序数组的函数，p 代表数组的起始位置，q 代表数组的末尾位置，r 代表的是数组的中间位置。
归并排序的动图演示：

归并排序的代码实现：

//归并排序
public static void mergeSort(int[] list,int p,int q, int[] temp){
	//验证左右节点不相等
    if(p < q){
        int r = (p + q)/2;//取中间节点
        mergeSort(list,p,r,temp);//排序左边数组list[p-r]
        mergeSort(list,r+1,q,temp);//排序右边数组list[r+1,q]
        merge(list,p,r,q,temp);//合并数组list[p-r] list[r+1,q]
    }
}

//合并
public static void merge(int[] list,int p, int r, int q, int[] temp){
    int i = p;//获取左边数组第一个元素下标
    int j = r + 1;//获取右边数组第一个元素下标
    int t = 0;//设定临时数组下标0
    while(i <= r && j <= q){
    	//左边元素小于右边元素
        if(list[i] <= list[j]){
            temp[t] = list[i];
            t++;
            i++;
        }else{
        	//左边元素大于右边元素
            temp[t] = list[j];
            t++;
            j++;
        }
    }
    //将左边剩余元素填充进temp中
    while(i <= r){
        temp[t] = list[i];
        t++;
        i++;
    }
 	//将右序列剩余元素填充进temp中
    while(j <= q){
        temp[t] = list[j];
        t++;
        j++;
    }
    t = 0;
    //将temp中的元素全部拷贝到原数组中
    while(p <= q){
        list[p] = temp[t];
        p++;
        t++;
    }
}

归并排序是稳定排序。当我们合并两边有序数组的时候，对比的两个元素值相等，那就先排左边数组元素再排右边数组元素，这样就能保证算法稳定。
关于时间复杂度的分析，王争老师给出了一个思路：递归求解的过程可以推导出递推公式，那么递归代码的时间复杂度一可以推导出递推公式。即问题 a 可以分解成问题 b 和 c 则解决问题 a 的时间复杂度就等于解决问题 b 和 c 的时间复杂度之和，公式为 T(a) = T(b) + T(c) + K，K 为合并 b 和 c 问题的时间复杂度。那么排序一个长度为 n 的数组，时间复杂度公式就是：T(n) = 2*T(n/2) + n，最后推导出时间复杂度为：O(nlogn)。推导过程我理解的也很生疏，就不总结出来了。最重要的是，根据这个分析问题的过程，我们了解到归并排序的时间复杂度跟数组的有序无序没关系，最好最坏以及平均时间复杂度都是O(nlogn)。
关于空间复杂度的计算并不想时间复杂度的计算那样需要累加。因为在任意时刻 CPU 只有一个函数再执行，也就是每次最多申请 n 个空间。当前函数执行结束后，立即释放掉了申请的内存空间，所以空间复杂度为 O(n)，归并排序不是原地排序。

快速排序

快速排序也叫快排，在待排序数组中任一选中一个元素，然后将数组中值比该元素小的放在左边，大的放在右边，然后再次对已经区分过大小的数组分别重复上述步骤，直到无法分割数组为止。
快速排序的核心思想可以理解为治分，最终的实现也是利用了递归。所以，我们先推导出递归公式：quick_sort(list[p,q]) = quick_sort(list[p,r]),quick_sort(list[r+1,q])，终止条件：p >= r。上述公式中，最关键的就是位置 r 的选取，r 一旦确定之后，再次调用 quick_sort 的时候 r 左右两边的元素分别是小于位置r的元素和大于位置r的元素。
快速排序的动图演示：

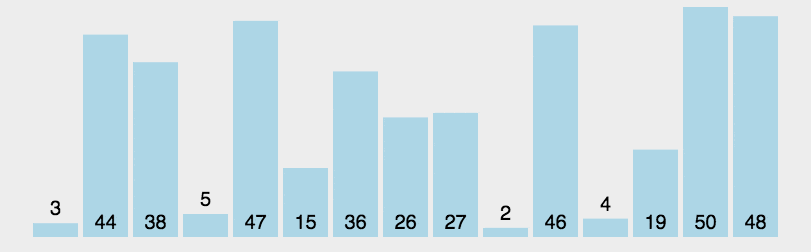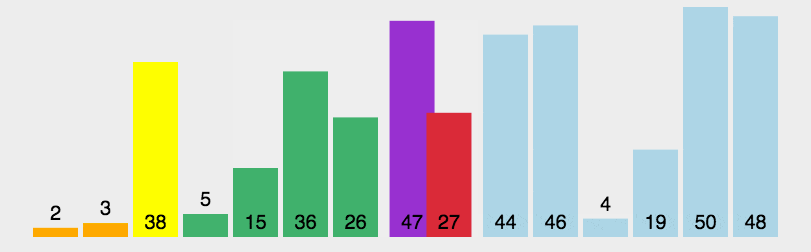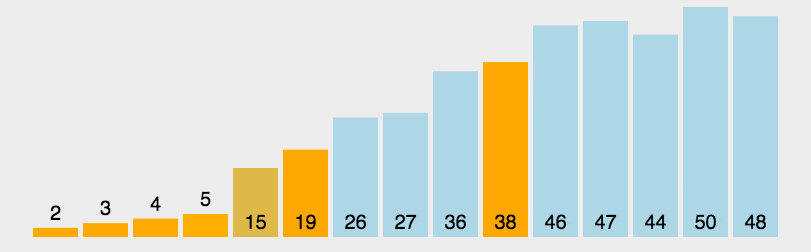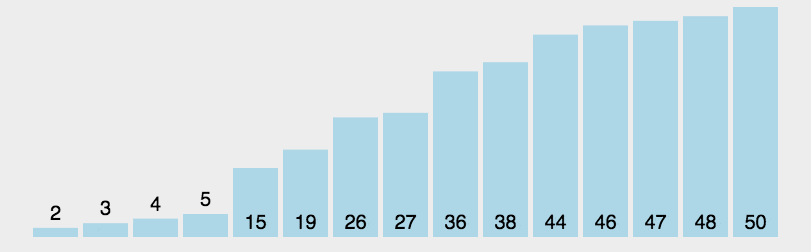
快速排序的代码实现：

//快速排序
public static void quickSort(int[] list, int p, int q){
	if(p < q){
    	int r = partition(list,p,q);
    	quickSort(list,p,r - 1);
    	quickSort(list,r + 1,q);
	}
}

//切点选取
public static int partition(int[] list, int p, int q){
	int i = p;
	int j = p;
	while(j < q){
		if(list[j] < list[q]){
			swap(list,i,j);
			i++;
		}
		j++;
	}
	swap(list,i,q);
	return i;
} 
//交换数组位置上的元素
public static void swap(int[] list, int i, int j){
	int temp = list[i];
	list[i] = list[j];
	list[j] = temp;
}

快速排序的时间复杂度推导跟归并排序的时间复杂度推导是一样的，所以最好和平均时间复杂度都是O(nlogn)，但是当我们考虑到极端情况，每次分组都是 1 和 n-1 个元素，则时间复杂度推导公式就是：T(n) = T(n-1)+ T(1) + n，然后复杂的推导，最后得出最坏时间复杂度是 O(n^2)。
快速排序在排序的过程中，空间复杂度为 O(1)，所以是原地排序。
由于排序过程中有数据插入操作，所以是一种不稳定的排序算法。

快速排序和归并排序对比

归并排序时间复杂度始终是O(nlogn)，但是由于不是原地排序，所以空间复杂度就高。快速排序，最好时间复杂度是O(nlogn)，最差是O(n^2)，但是却是原地排序，空间复杂度低。所以，如果恰当的选择快速排序的切入点，那么快排的执行效率是高于归并排序的。
理解这两种排序的思路，还是需要好好理解分治思想，理解递归的推导和实现。

总结

初入算法学习，必是步履蹒跚，一路磕磕绊绊跌跌撞撞。看不懂别慌，也别忙着总结，先读五遍文章先，无他，唯手熟尔~
与诸君共勉
这篇文章写了三个小时。。。着实很难理解啊。。。