冒泡排序，选择排序，插入排序

本文创作灵感来源于极客时间王争老师的《数据结构与算法之美》课程，通过课后反思以及借鉴各位学友的发言总结，现整理出自己的知识架构，以便日后温故知新，查漏补缺。

如何分析一个排序算法

排序算法的执行效率

最好情况，最坏情况，平均时间复杂度。待排序数据的有序度对于排序算法的执行效率有着明显的影响，所以需要区分这三个时间复杂度。
比较时间复杂度的系数，常数，低阶。在分析时间复杂度的时候，我们是把这三项给省略了，这是基于数据量 n 无限大的情况。但是在实际情况下，我们待排序的数据一般都很小，这个时候上述三者的影响就比较大，不能再忽略不计了。
比较次数和交换次数。排序算法中必不可少的就是比较和交换移动数据的操作，所以在考虑算法的效率的时候，我们需要考虑这两种操作带来的影响。

排序算法的内存消耗

排序算法涉及到元素的交换移动，所以我们需要考虑到空间复杂度。引出一个概念：原地排序。原地排序就是指不申请多余的空间来进行的排序，就是在原来的排序数据中比较和交换的排序。希尔排序、冒泡排序、插入排序、选择排序、堆排序、快速排序都属于原地排序。

排序算法的稳定性

除了排序效率和内存占用两个指标外，还有一个稳定性的概念来衡量排序算法的优劣。排序稳定性：待排序数组中，相同值得元素，排序前和排序后两者的相对排序不会发生改变。举例：两个元素值都是 7，排在前一位的记为 7(1)，后一位记为 7(2)。排序后，7(1) 依然排在 7(2) 前面，这就是稳定排序。

三种稳定排序算法

冒泡排序

冒泡排序的思路：每次在数据的待排序区间选定一个元素，将其与其他元素比较大小，最后确定最值，将其依次排在有序区间。
排序动图如下：

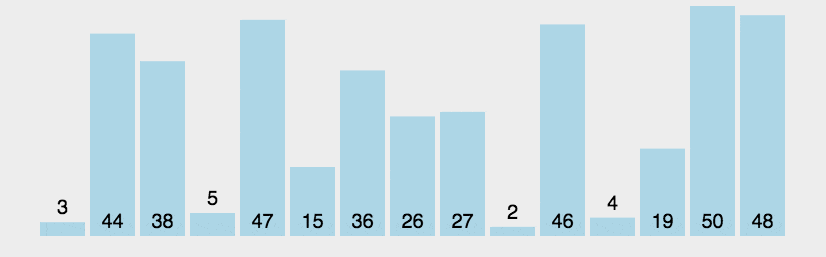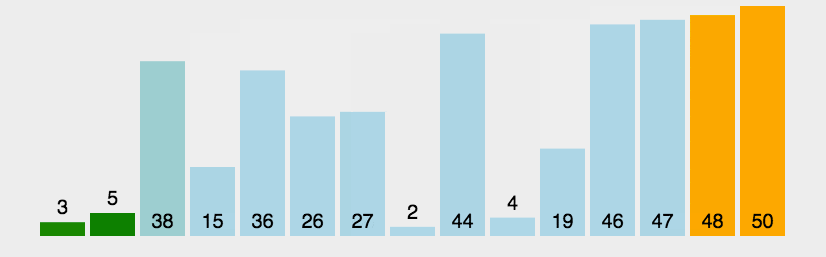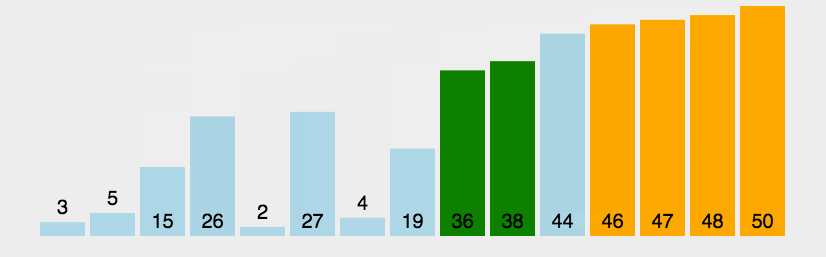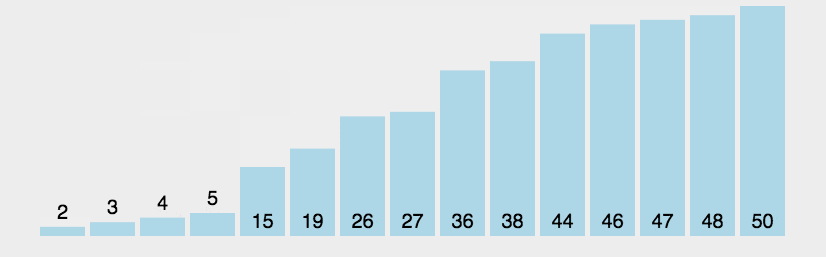
代码如下：

//冒泡排序
public void bubbleSort(int[] list){
    for(int i = 0; i < list.length; i++){
        //提前终止标识
        boolean flag = true;
        for(int j = 0; j < list.length - i - 1; j++){
            if(list[j] > list[j + 1]){
                int item = list[j + 1];
                list[j + 1] = list[j];
                list[j] = item;
                flag = false;
            }
        }
        if(flag){
            break;
        }
    }
}

在上述代码中，我们添加了一个标识变量 flag。每次冒泡开始前设置 flag 的值为 true，在冒泡的过程中，如果发生元素交换，就改变 flag 值为 flase。则，冒泡结束的时候，如果 flag == true 说明本次冒泡没有发生元素交换，说明数组已经有序，可以直接终止后续冒泡，提高了冒泡算法的执行效率。

冒泡排过程中只会交换相邻两个元素的位置，只需要常量级别的临时内存空间，所以空间复杂度为 O(1)，是原地排序。在冒泡排序中，如果两个元素的值相同，那么我们不进行交换，则该排序也是稳定性排序。

冒泡排序最好时间复杂度为 O(n)，最坏时间复杂度为 O(n^2)，那么怎么分析平均时间复杂度呢。按照上述冒泡排序代码，由于有了 flag 标识变量，就导致了冒泡的次数小于等于 n 次，而最终决定冒泡次数的是元素的有序度和无无序度。

有序度：数组中具有有序关系的元素对的个数。即：a[i] <= a[j]，i < j。
逆序度：数组中具有无序关系的元素对的个数。即：a[i] > a[j]，i < j。

举例：在数组 [1，3，2，6，5] 中，有序度为 8：(1,3)(1,2)(1,6)(1,5)(3,6)(3,5)(2,6)(2,5)；逆序度为 2：(3,2)(6,5)。
在有序数组 [1，2，3，5，6] 中，有序度为 10，也叫做满有序度。
总结规律：在一个待排序数组中，满有序度 = 有序度 + 逆序度。满有序度 =n*(n-1)/2。下面给出数组 [4，5，6，3，2，1] 冒泡过程中有序度和无序度的变化。

冒泡次数	冒泡结果	有序度	交换次数
初始状态	[4，5，6，3，2，1]	3	0
第1次冒泡	[4，5，3，2，1，6]	6	3
第2次冒泡	[4，3，2，1，5，6]	9	3
第3次冒泡	[3，2，1，4，5，6]	12	3
第4次冒泡	[2，1，3，4，5，6]	14	2
第5次冒泡	[1，2，3，4，5，6]	15	1

我们观察得出结论，元素每交换一次，有序度增加一次。那么得出最好情况下，需要交换 0 次，最坏的情况下，需要交换 n(n-1)/2 次，取个中间值 n(n-1)/4。在排序过程中，比较次数远远大于交换次数，但是总的时间复杂度不会高于 O(n^2)，所以平均时间复杂度为 O(n^2)。

插入排序

插入排序的思路：每次在数据的待排序区间选定一个元素，将其与有序区间的元素依次比较大小，确定最后插入位置。
排序动图如下：

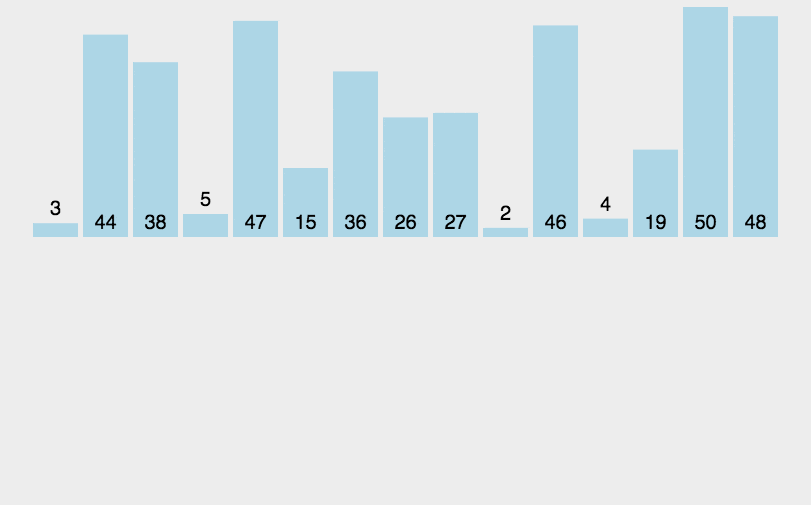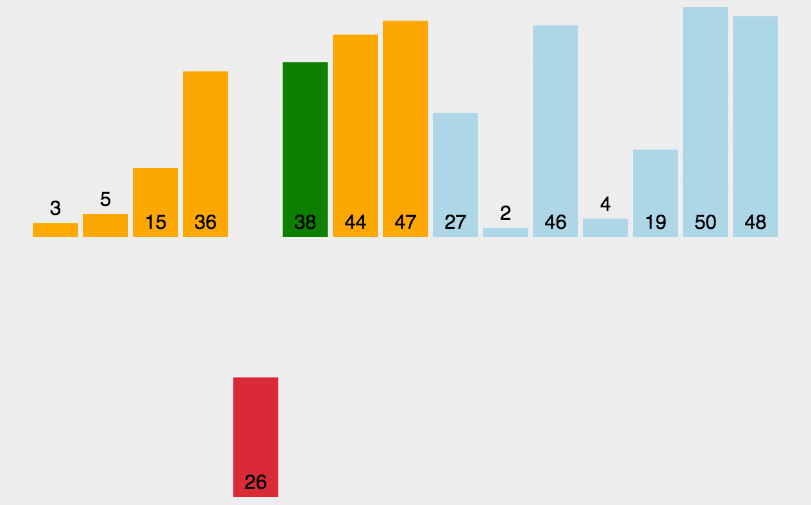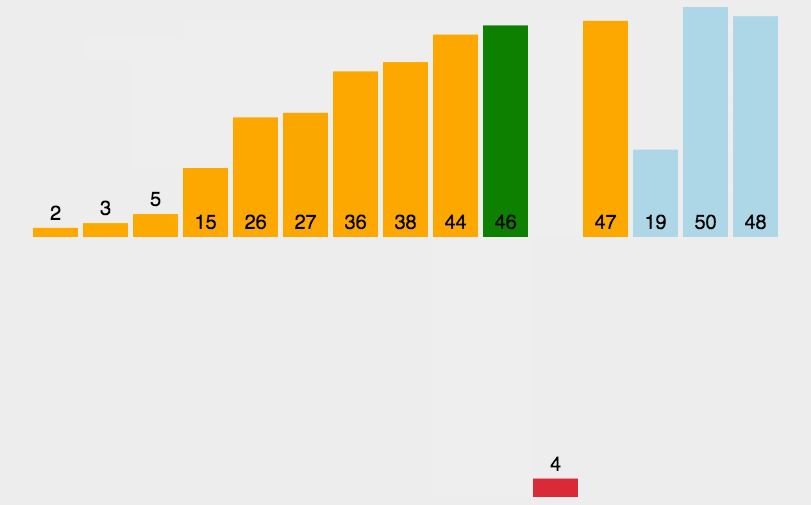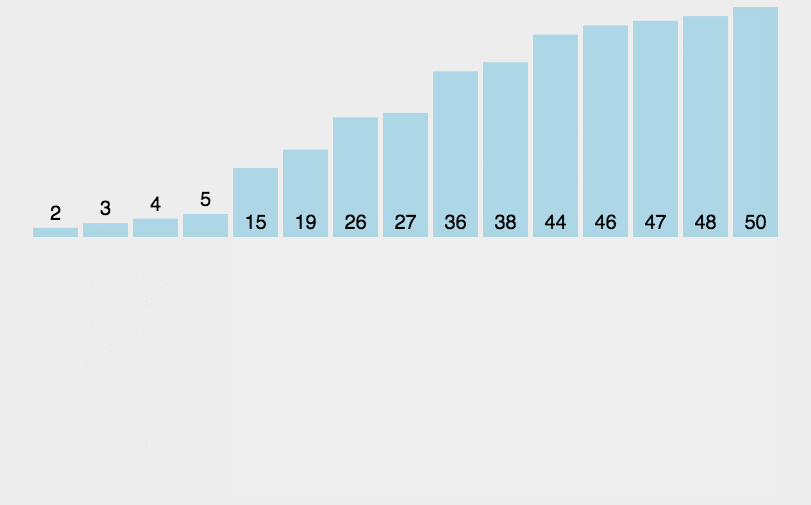
代码如下：

//插入排序
public static void insertSort(int[] list){
    for(int i = 1; i < list.length; i++){
        int item = list[i];
        int j = i - 1;
        for(; j >= 0; j--){
            if(item < list[j]){
                list[j + 1] = list[j];
            }else {
                break;
            }
        }
        list[j + 1] = item;
    }
}

从上述代码中看出，插入排序并不需要额外的空间，所以是原地排序。在擦插入排序中，对于相等的元素不进行交换位置，则也是稳定的排序。插入排序的时间复杂度，对于一个有序的数组，只需遍历一遍数组，最好时间复杂度为 O(n)，对于逆序的数组，相当于执行便利数组 n 次，每次都在数组前面插入元素，则最坏时间复杂度为 O(n^2)。平均时间复杂度，在数组中插入一个元素的平均时间复杂度为 O(n)，那么执行 n 次，平均时间复杂度就是 O(n^2)；

选择排序

选择排序的思路：每次在数据的待排序区间选定最值元素，然后将其与靠近有序区间的第一个元素交换位置。
排序动图如下：

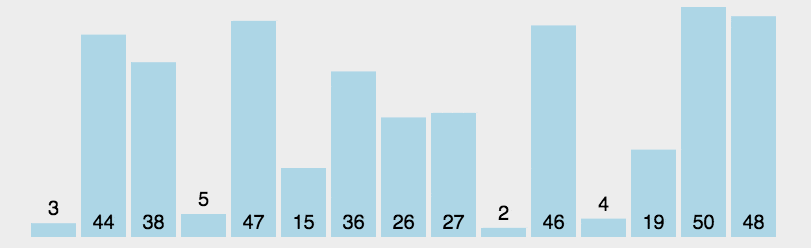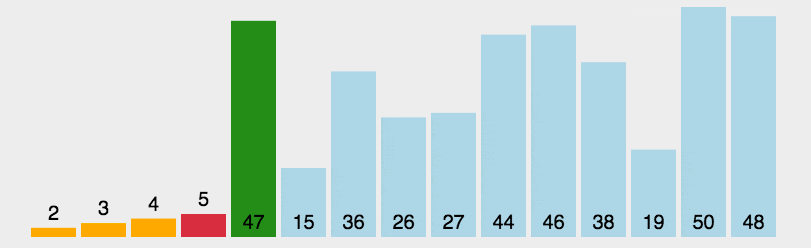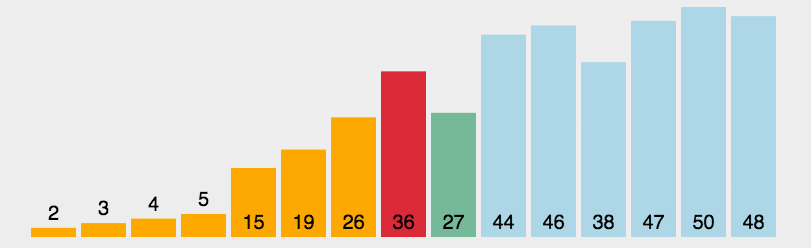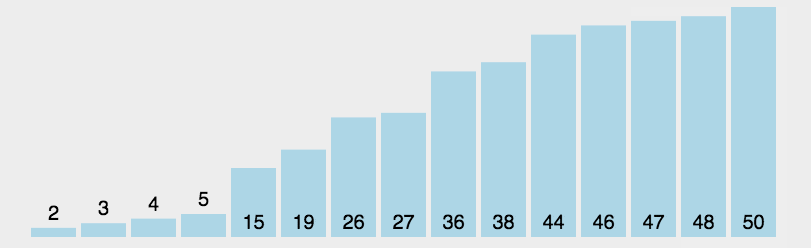
代码如下：

//选择排序
public static void selectSort(int[] list){
    for(int i = 0; i < list.length; i++){
        int index = i;
        for(int j = i; j < list.length; j++){
            if(list[index] > list[j]){
                index = j;
            }
        }
        int item = list[index];
        list[index] = list[i];
        list[i] = item;
    }
}

选择排序只需要常量级别的临时内存空间，所以空间复杂度为 O(1)。最好时间复杂度为 O(n)，最坏时间复杂度为 O(n^2)，平均时间复杂度与插入排序分析方法一样，也是O(n^2)。由于选择排序并非相邻元素交换位置，所以不是稳定排序。

比较插入排序和冒泡排序

冒泡排序和插入排序无论如何优化，冒泡排序元素交换的次数和插入排序元素的移动次数都是等于元数据的逆序度。但是从代码实现上，冒泡排序元素交换时的代码复杂度高于插入排序元素移动时的代码复杂度，所以从性能上，插入排序的执行效率要高于冒泡排序。

总结

初入算法学习，必是步履蹒跚，一路磕磕绊绊跌跌撞撞。看不懂别慌，也别忙着总结，先读五遍文章先，无他，唯手熟尔~
与诸君共勉